Convoluzione

Come anticipato nell’articolo “Toolbox per studiare DSP”, un segnale è un oggetto che trasporta l’informazione riguardante la variazione di una variabile rispetto ad un’altra di riferimento. Nel caso dei segnali audio: il modo in cui varia l’ampiezza del suono rispetto al tempo.

I segnali possono essere di infinite tipologie, ma ce ne sono alcuni ben noti, semplici e particolarmente ricorrenti. Concentriamoci al momento su uno in particolare: l’impulso di Dirac \(δ(t)\). E’ un segnale \(=0\) su tutti gli istanti temporali tranne che su un singolo punto, in cui idealmente vale infinito. Dal punto di vista sonoro, potremmo immaginarlo come un click molto forte in ampiezza e temporalmente molto corto.

Immaginiamo di essere in una grande stanza vuota e di emettere questo click attraverso uno speaker. Cosa accade? Beh, inizialmente le nostre orecchie verranno raggiunte dal segnale diretto emesso dallo speaker. Dopo poco tempo, arriveranno le riflessioni primarie, e successivamente una coda di riflessioni secondarie. Possiamo immaginare la situazione più o meno così:

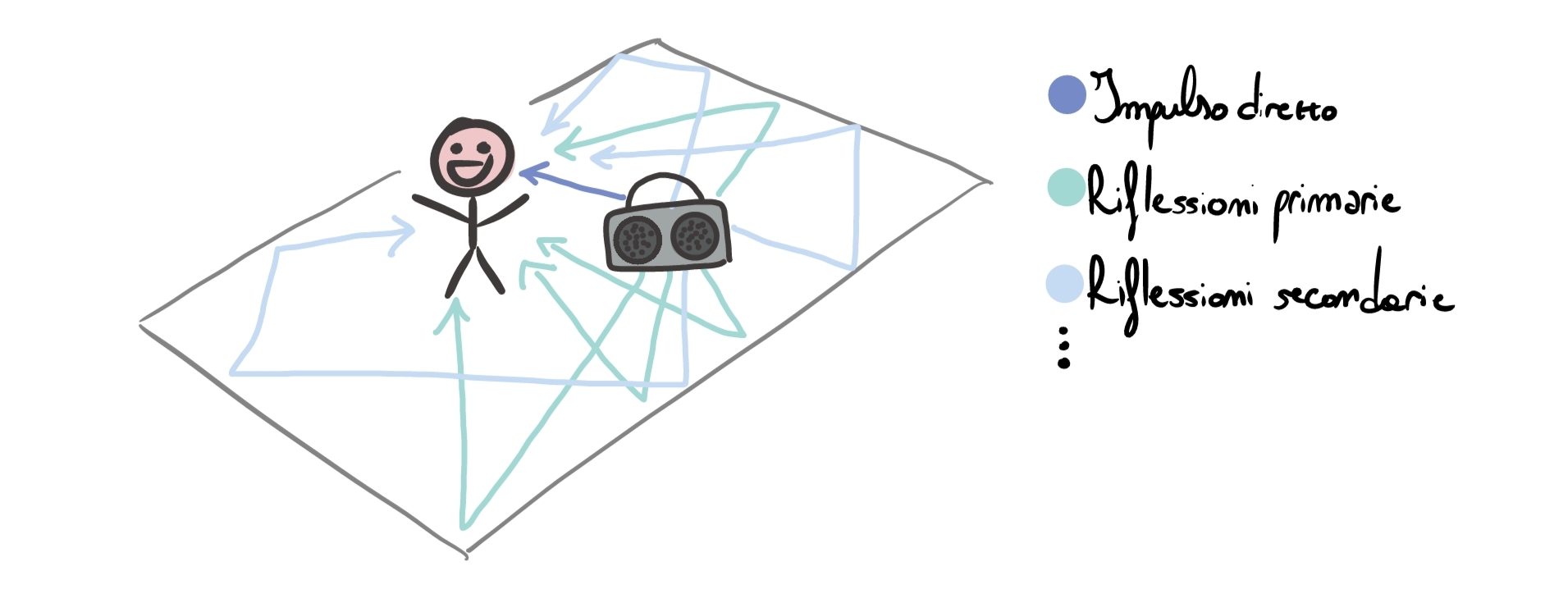
Immaginiamo di posizionare un microfono al posto dell’ascoltatore (tralasciamo al momento la questione direzionalità, attenuazione ed ogni altra complicazione) e di registrare il risultato dell’emissione dell’impulso nella stanza: otterremo un file audio rappresentante proprio l’impulso diretto + le varie riflessioni. Questa registrazione è detta Impulse Response ed è l’impronta digitale del sistema “stanza”. E’ possibile in seguito usare l’IR \(=h(t)\) per emulare la stanza, in questo modo:

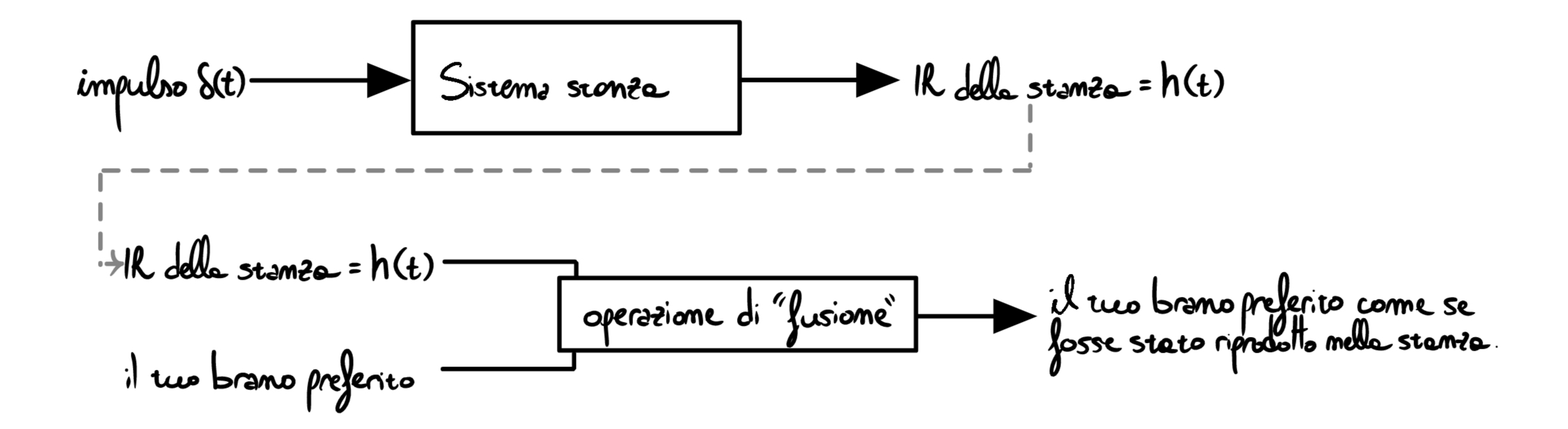
impulso

L’operazione di fusione nell’immagine sopra è l’argomento che guiderà il resto dell’articolo: la convoluzione.

La convoluzione

Immaginiamo di voler applicare l’Impulse Response ottenuto dalla registrazione precedente ad un singolo clap di mani \(x(t)\).

Pensiamo bene alle differenze tra il segnale originale \(x(t)\) e quello modificato \(y(t)\) che vogliamo ottenere:

\(x(t)\) contiene il singolo clap di mani, poi silenzio.
\(y(t)\) contiene lo stesso clap di mani, e poi le riverberazioni, ovvero ripetizioni del clap iniziale, ritardate nel tempo e attenuate in ampiezza, che creano “l’illusione che il clap sia stato emesso nella stanza”.

In pratica \(y(t)\) è il risultato dell’applicazione di una legge che trasforma il segnale \(x(t)\) in un nuovo \(y(t)\), combinando i campioni passati e presenti del segnale originale. In matematichese, nel dominio discreto: \(y[n]=\sum_{k=-\infty}^{+\infty} x[k]\cdot h[n-k]\), dove \(h\) è proprio l’IR (il filtro) che stiamo applicando. L’operazione descritta dalla formula precedente è detta convoluzione e viene indicata col simbolo \(*\).

Calcolare la convoluzione \(y[n]=x[n]*h[n]\) di due segnali è noioso, lungo, ripetitivo e dispendioso, ma anche concettualmente semplice. Consideriamo per esempio:

il segnale \(x(n)=3\delta[n]+3\delta[n-1]+3\delta[n-2]\)
un filtro \(h(n) = \delta[n]-1\delta[n-1]+5\delta[n-2]\)

il filtraggio più essere effettuato attraverso il seguente algoritmo:

“Invertiamo” \(h(n)\), ottenendo \(h(-n)\).

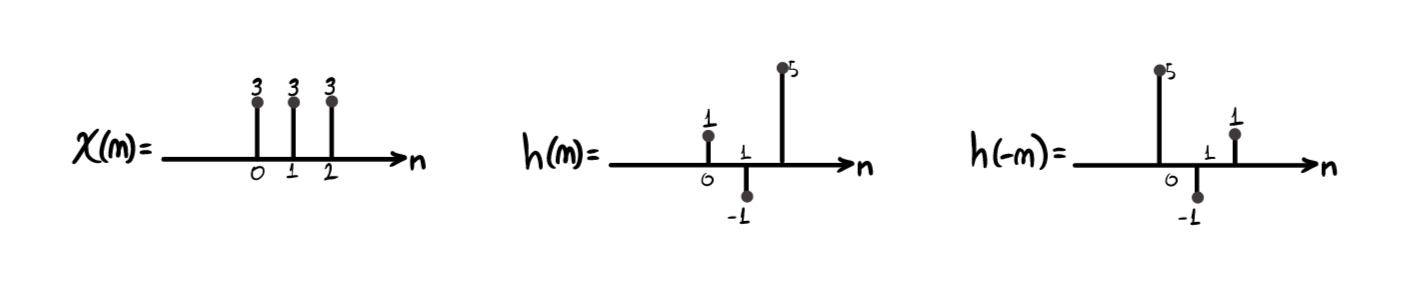
“Prendiamo” \(h(-n)\) e, per ogni posizione possibile, la trasliamo da sinistra (\(-\infty\)) a destra (\(+\infty\)), effettuando la moltiplicazione sample per sample tra \(x(n)\) e \(h(n)\). Poi, sommiamo i risultati parziali ottenuti (ovviamente, non è necessario partire realmente da \(-\infty\); basta partire dalla prima posizione per cui \(x(n)\) e \(h(-n)\) hanno un sample sovrapposto). Ognuna di queste traslazioni ci restituirà un sample del nuovo segnale di output \(y(n)\), risultato della convoluzione.

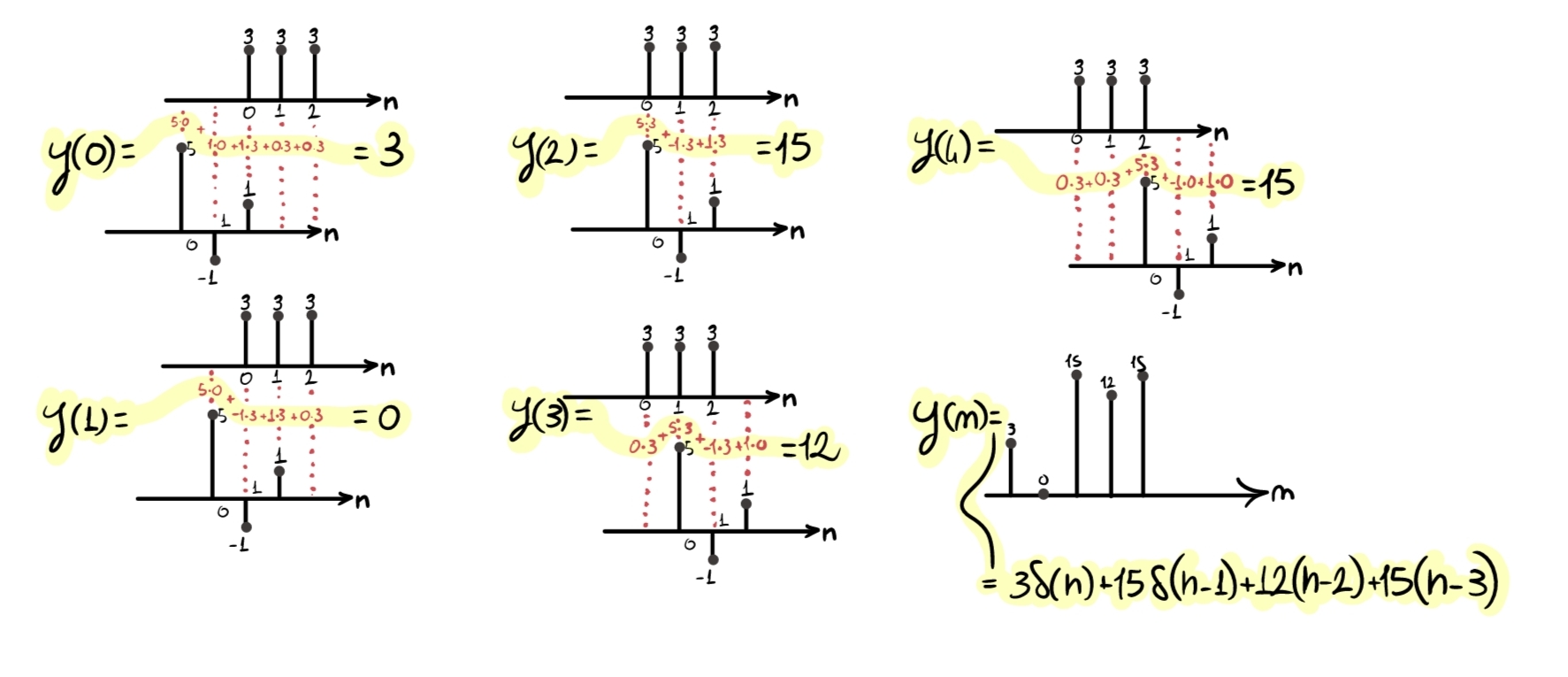
La convoluzione svolta in questo modo è molto dispendiosa in termini di risorse computazionali, per cui non è assolutamente adatta ad ambienti poco potenti o sistemi che devono funzionare in real time. La soluzione a questo problema la vedremo in un capitolo successivo.

Per questa operazione valgono interessanti proprietà. Quelle che secondo me vale la pena ricordare per la “quotidianità” sono: commutativa, associativa, linearità, tempo-invarianza.

Proprio quest’ultima proprietà farà da transizione tra questo argomento e il successivo.

Sistemi LTI, esponenziale complesso e dominio in frequenza

(Semplificando) un sistema \(T\) il quale, a partire da un input \(x[n]\), produce un output \(y[n]=T\{x[n]\}\), è tempo-invariante se una traslazione del tempo dell’input porta come unica conseguenza una (stessa) traslazione temporale dell’output, ovvero se \(T\{x[n-n_0]\} = y[n-n_0]\).

Un sistema è invece lineare se non introduce non-linearità nell’output, ovvero se valgono i seguenti due principi:

Additività: la risposta alla somma è la somma delle risposte. -> \(T\{x_1[n]+x_2[n]\}=T\{x_1[n]\}+T\{x_2[n]\}\)
Scalabilità: la risposta a un segnale scalato è scalata uguale. -> \(T\{\alpha x[n]\}=\alpha\,T\{x[n]\}\)

Ovviamente, un sistema Lineare Tempo-Invariante (LTI) gode di tutte le proprietà appena citate: \(y[n] = (h*x)[n] = \sum_{k=-\infty}^{\infty} h[k]\;x[n-k]\).

Adesso, consideriamo l’esponenziale complesso \(e^{j\omega n}\), che per l’identità di Eulero vista in questo articolo è pari alla somma di sinusoidi \(e^{j\omega n}=\cos(\omega n)+j\sin(\omega n)\).

Prendiamo un sistema LTI con risposta all’impulso \(h[n]\). Abbiamo visto che la sua uscita è calcolabile tramite la convoluzione \(y[n]=\sum_{k=-\infty}^{+\infty} h[k]\;x[n-k]\). Imponendo come ingresso \(x[n]=e^{j\omega n}\) e sostituendo nella formula, otteniamo:

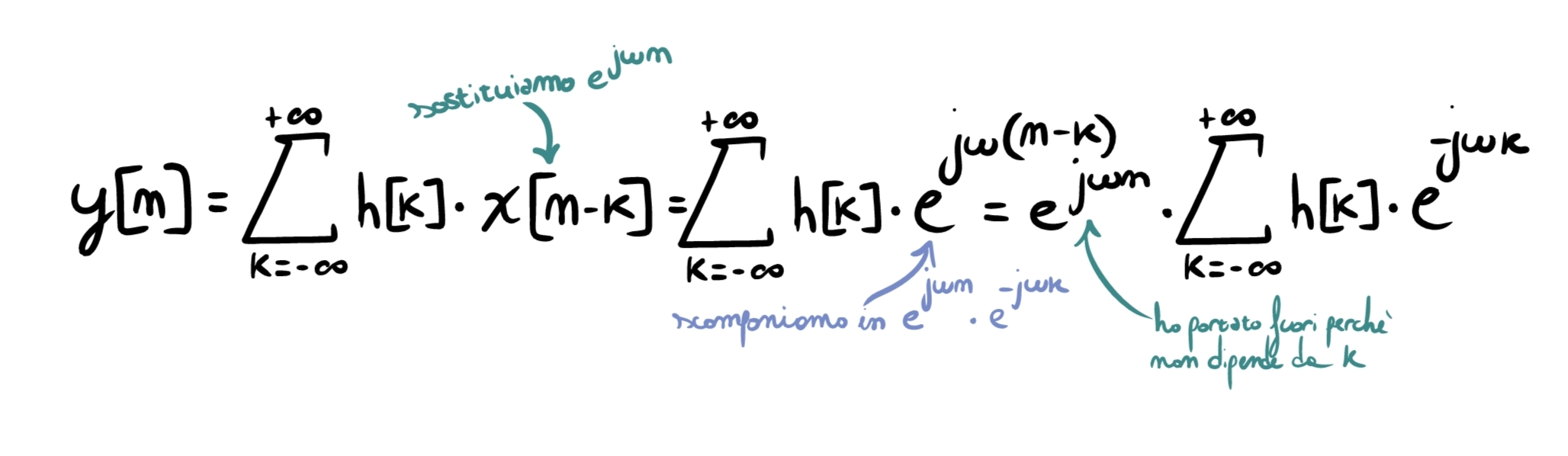
Come si può vedere, il termine \(\sum_{k=-\infty}^{+\infty} h[k]\,e^{-j\omega k}\) non è in alcun modo dipendente dal tempo \(n\), ma soltanto dal filtro (\(k\)). Definiamo questa quantità come \(H(e^{j\omega})=\sum_{k=-\infty}^{+\infty} h[k]\,e^{-j\omega k}\): è la risposta in frequenza del sistema, ovvero la risposta del sistema quando riceve in input sinusoidi pure ad una frequenza \(\omega\) (in questo caso, abbiamo dato in input \(e^{j\omega n}=\cos(\omega n)+j\sin(\omega n)\)). Da adesso in poi, lavoreremo molto con questo concetto.

Tornando al caso attuale, possiamo quindi riscrivere l’equazione come \(y[n]=e^{j\omega n}\,H(e^{j\omega})\). Notiamo diverse cose importanti:

la forma del segnale in uscita è ancora \(e^{j\omega n}\);
il sistema non crea nuove frequenze;
tutto ciò che fa è moltiplicare il segnale per un numero complesso.

Per questo si dice che \(e^{j\omega n}\) è un’autofunzione dei sistemi LTI.

Capisco che tutto ciò sembra una complicazione assurda senza uno scopo preciso, ma vedremo che così non è.

Me cumpari Fourier

Fino a questo punto abbiamo visto che un sistema LTI ha una proprietà fondamentale: se in ingresso mettiamo un esponenziale complesso \(e^{j\omega n}\), in uscita otteniamo la stessa forma, moltiplicata per un numero complesso \(H(e^{j\omega})\).

Questa osservazione, da sola, non basta. La domanda naturale è: perché questo dovrebbe aiutarci a descrivere segnali reali, che non sono affatto esponenziali complessi?

Un segnale reale non è una singola sinusoide, non ha una sola frequenza e varia nel tempo in modo complesso. Tuttavia, esiste un fatto fondamentale: qualunque segnale può essere visto come somma di tante componenti elementari, ognuna oscillante a una propria frequenza. Queste componenti elementari sono proprio gli esponenziali complessi \(e^{j\omega n}\).

In altre parole, invece di descrivere un segnale nel tempo come “una forma complicata”, possiamo descriverlo come una collezione di frequenze, ciascuna con una certa ampiezza e una certa fase. Questa è l’idea alla base della rappresentazione di Fourier.

Se inoltre ipotizziamo di lavorare su sistemi LTI, vale il principio di sovrapposizione:

la risposta alla somma è la somma delle risposte
la risposta a un segnale scalato è scalata nello stesso modo

Questo significa una cosa molto potente: se conosco la risposta del sistema a ciascuna componente elementare, conosco la risposta al segnale completo.

Se un segnale è somma di tante sinusoidi, e il sistema risponde a ogni sinusoide moltiplicandola per \(H(e^{j\omega})\), allora l’uscita sarà semplicemente la somma di tutte queste sinusoidi modificate. Non serve fare nulla “in più”.

Se nel dominio del tempo il filtraggio richiedeva una convoluzione: \(y[n]=\sum_{k=-\infty}^{+\infty} h[k]\;x[n-k]\) (molto costosa), nel dominio delle frequenze ogni componente in frequenza del segnale viene trattata indipendentemente, venendo semplicemente moltiplicata per un numero complesso.

Anticipiamo il risultato: convolvere nei tempi corrisponde a moltiplicare in frequenza.

Perché questo è utile? Semplicemente perché moltiplicare è infinitamente meno costoso che convolvere. Questo è il motivo per cui spesso analizziamo i sistemi nel dominio della frequenza, progettiamo filtri guardando \(H(e^{j\omega})\) e usiamo Fourier e FFT (che vedremo a breve) nel processamento audio reale.

Serie di Fourier

Vincoliamoci per ora al caso dei segnali discreti periodici. In particolare, consideriamo un segnale discreto periodico \(x[n]\) di periodo \(N\): \(x[n] = x[n+N]\).

Questo vincolo ha una conseguenza fondamentale: anche le frequenze che lo compongono devono essere periodiche, e quindi assumere solo valori ben precisi.

Nel dominio discreto, le uniche esponenziali complesse compatibili con la periodicità \(N\) sono quelle per cui \(e^{j\omega (n+N)} = e^{j\omega n}\):

per cui le frequenze ammesse non sono continue, ma discrete.

Visto tutto ciò, un segnale periodico \(x[n]\) può essere scritto attraverso la la Serie di Fourier discreta \(x[n] = \sum_{k=0}^{N-1} X[k]\;e^{j\frac{2\pi}{N}kn}\), nella quale:

\(e^{j\frac{2\pi}{N}kn}\) sono le componenti sinusoidali di base;
\(X[k]\) sono coefficienti complessi;
\(N\) è il periodo del segnale.

Questa formula dice che il segnale nel tempo è una combinazione lineare di sinusoidi a frequenze multiple della fondamentale \(\frac{2\pi}{N}\). I coefficienti \(X[k]\) nella formula si ottengono tramite: \(X[k] = \frac{1}{N}\sum_{n=0}^{N-1} x[n]\;e^{-j\frac{2\pi}{N}kn}\).

Non serve memorizzare questa formula ora: serve solo per capire che ogni coefficiente misura “quanto” di quella frequenza è presente e che il segnale è completamente descritto dall’insieme dei \(X[k]\).

Fisicamente, ogni termine della somma \(X[k]\;e^{j\frac{2\pi}{N}kn}\) rappresenta una sinusoide con pulsazione \(\omega_k = \frac{2\pi}{N}k\), ampiezza \(\|X[k]\|\) e fase \(\angle X[k]\). Nel dominio della frequenza, a ogni k corrisponde una riga spettrale e quindi lo spettro è una sequenza discreta di impulsi.

Trasformata di Fourier

La Serie di Fourier ci ha permesso di descrivere segnali discreti periodici come somma di sinusoidi a frequenze discrete. Tuttavia, la maggior parte dei segnali reali non è periodica: una parola pronunciata, un colpo di rullante, un clap di mani o un qualsiasi evento sonoro isolato non si ripete identico nel tempo.

Cosa succede, quindi, se rimuoviamo il vincolo di periodicità?

Quando un segnale non è periodico, non esiste più un periodo N che imponga una griglia sulle frequenze ammesse e, di conseguenza, lo spettro non è più costituito da righe discrete, ma diventa continuo. In questo caso, la rappresentazione del segnale nel dominio delle frequenze è fornita dalla Trasformata di Fourier discreta nel tempo: \(X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n]\;e^{-j\omega n}\).

Dal punto di vista concettuale:

\(x[n]\) descrive cosa accade nel tempo;
\(X(e^{j\omega})\) descrive quanta energia è presente a ciascuna frequenza e con quale fase.

Anche in questo caso, \(X(e^{j\omega})\) è una quantità complessa. Il suo modulo \(\|X(e^{j\omega})\|\) indica l’ampiezza delle componenti in frequenza, mentre l’argomento \(\angle X(e^{j\omega})\) indica la fase.

A differenza della Serie di Fourier, qui \(\omega\) varia in modo continuo. Questo significa che lo spettro non è più una sequenza di righe, ma una funzione continua della frequenza.

Da notare che passare dal dominio del tempo al dominio della frequenza comporta un compromesso: nel dominio del tempo sappiamo quando accadono gli eventi, in frequenza sappiamo di che frequenze sono fatti. Questo vuol dire che la Trasformata di Fourier fornisce una descrizione globale del segnale: dice quali frequenze sono presenti e con quale peso, ma non conserva l’informazione temporale puntuale. Non sappiamo più in quale istante una certa componente è apparsa, ma solo che è presente nel segnale complessivo.

Ci sono quindi casi in cui conviene lavorare nei tempi, e casi in cui è conveniente passare in frequenza.

Convoluzione e moltiplicazione: la proprietà fondamentale

A questo punto abbiamo introdotto due concetti che sembrano vivere in mondi diversi:

nel dominio del tempo, un sistema LTI filtra tramite convoluzione;
nel dominio della frequenza, un segnale è descritto dal suo spettro \(X(e^{j\omega})\).

Il punto centrale dell’articolo è che questi due mondi sono legati da una proprietà estremamente potente:

\[y[n] = x[n] * h[n] \quad \Longleftrightarrow \quad Y(e^{j\omega}) = X(e^{j\omega}) \cdot H(e^{j\omega})\]

Questa relazione va letta così: se nel tempo l’uscita è la convoluzione tra input \(x[n]\) e risposta all’impulso \(h[n]\), allora in frequenza lo spettro dell’uscita \(Y(e^{j\omega})\) si ottiene semplicemente moltiplicando lo spettro dell’ingresso \(X(e^{j\omega})\) per la risposta in frequenza del filtro \(H(e^{j\omega})\).

In pratica, filtrare un segnale significa “modellare” il suo contenuto in frequenza: \(Y(e^{j\omega}) = X(e^{j\omega}) \cdot H(e^{j\omega})\).

Se per una certa \(\omega\) il filtro ha \(\|H(e^{j\omega})\|\) piccolo, quella frequenza viene attenuata. Se \(\|H(e^{j\omega})\|\) è grande, viene amplificata. La fase \(\angle H(e^{j\omega})\) invece descrive quanto quella componente viene sfasata.

Come già detto, convolvere nel tempo significa che per ogni campione \(n\) è necessario eseguire molte moltiplicazioni e molte somme. Se \(h[n]\) ha \(M\) campioni “utili”, allora per ogni campione di uscita servono circa \(M\) moltiplicazioni e \(M-1\) somme. Su segnali lunghi, o in real time, questo diventa rapidamente pesante.

Nel dominio della frequenza, invece, lo stesso filtraggio diventa una moltiplicazione punto per punto: \(Y(e^{j\omega}) = X(e^{j\omega}) \cdot H(e^{j\omega})\).

Concettualmente è molto più semplice: ogni frequenza viene trattata in modo indipendente e non c’è “mescolamento” diretto tra campioni nel tempo.

Discrete Fourier Transform (DFT)

Finora abbiamo parlato di Serie e Trasformata di Fourier in modo “ideale”, cioè assumendo sequenze infinite e somme che vanno da \(-\infty\) a \(+\infty\). È utile per capire i concetti, ma un file audio, una registrazione o un buffer in un plugin sono tutti array di campioni con lunghezza limitata. Per questo, nella pratica, non possiamo calcolare direttamente la Fourier Transform come vista sopra.

Quello che facciamo davvero è prendere il segnale finito ed ipotizzare che sia periodico, ovvero che si ripeta sempre uguale con periodo \(N\) pari alla sua durata.

Dato un blocco di N campioni \(x[0],x[1],\dots,x[N-1]\), la Discrete Fourier Transform (DFT) definisce N campioni di spettro X[k], dove k è l’indice di frequenza: \(X[k] = \sum_{n=0}^{N-1} x[n]\;e^{-j\frac{2\pi}{N}kn}\), con \(k=0,1,\dots,N-1\).

Questa formula dice tre cose importanti:

Lo spettro è discreto -> non otteniamo una funzione continua di \(\omega\), ma \(N\) valori \(X[0],X[1],\dots,X[N-1]\). Ogni \(k\) corrisponde a una frequenza campionata su una griglia.
Lo spettro è periodico -> la DFT descrive il contenuto in frequenza di un blocco finito assumendo, implicitamente, che quel blocco si ripeta nel tempo. È lo stesso motivo per cui la Serie di Fourier nasce dai segnali periodici. Qui la periodicità non è “reale”, è un’ipotesi matematica che rende possibile la trasformata su dati finiti.
Ampiezza e fase ci sono ancora -> anche X[k] è complesso: \(\|X[k]\|\) dice quanto è presente la frequenza \(k\) mentre \(\angle X[k]\) ne descrive la fase.

Fast Fourier Transform (FFT)

La formula della DFT sembra innocua, ma richiede molte operazioni. Se si calcola a forza bruta, per ottenere tutti gli \(X[k]\) servono dell’ordine di \(N^2\) moltiplicazioni e somme.

Per \(N\) grande (tipico in audio), questo è pesante.

La FFT risolve proprio il problema appena esposto. Non è una trasformata diversa dalla DFT, ma un modo intelligente di calcolare la stessa identica trasformata con un numero di operazioni drasticamente minore (invece di crescere come \(N^2\), cresce circa come \(N\log_2 N\)).

Non approfondirò qui l’algoritmo di calcolo nello specifico, basti sapere che è questa la funzione che si usa solitamente nel codice reale (spesso si ha una funzione di libreria già pronta, del tipo fft(qualcosa,altriparametri) ).

Torniamo all’esempio del clap

Possiamo finalmente applicare l’IR della stanza iniziale al nostro clap, in maniera più efficiente della convoluzione nei tempi. I passaggi in ordine di esecuzione sono:

FFT del segnale rappresentante il clap \(x[n]\);
FFT della IR \(h[n]\);
moltiplicazione punto per punto in frequenza tra \(X[k]\) e \(H[k]\);
IFFT del risultato \(Y[k]\) per tornare nel tempo, ottenendo \(y[n]\).

Ed è così che si fa convoluzione veloce. O meglio, è già qualcosa, ma questa tecnica non è ancora adatta ad applicazioni complesse in real time. Per far ciò è necessario partizionare in qualche modo la convoluzione. Vedremo metodi per far ciò nell’articolo sulla convoluzione RT.

Angelo Antona, 6 DICEMBRE 2025