Convoluzione real time

La semplice convoluzione tramite DFT o FFT vista nell’articolo sulla convoluzione è già una soluzione molto più efficiente del processamento nel tempo, ma per i real-time cases non è ancora abbastanza.

Immaginiamo di voler costruire un pedale digitale per chitarra. Questo ha un jack in entrata, a cui colleghiamo lo strumento, e un jack in uscita per l’output verso i diffusori. L’obiettivo non è ovviamente quello di registrare l’intero brano e poi, successivamente, applicare con calma il nostro bel IR e ottenere il segnale filtrato: è necessario che, man mano che i sample arrivano, si processi il segnale mandando subito “qualcosa in uscita”. La latenza deve essere impercettibile.

E’ questo uno dei casi d’uso degli algoritmi che spiegherò in questo articolo.

Conv con partizionamento del segnale in input

Tornando all’esempio del pedale per chitarra, un modo intuitivo per poter processare un segnale in real time è quello di spezzettare l’input in tanti blocchi temporali lunghi \(L\): man mano che l’audio in input arriva, noi lo accumuliamo in un buffer che rappresenta il frame e, quando il frame è pieno, lo processiamo e lo mandiamo in output, iniziando al contempo l’accumulo del frame successivo.

Sarebbe tutto molto semplice, se non fosse che nella convoluzione i frames del segnale passato continuano ad avere effetto sul segnale corrente. Immaginiamo poprio l’esempio del riverbero: il frame in uscita al tempo \(t\) è costituito dal frame in input al tempo \(t-1\) sommato alle riverberazioni dei frames precedenti (più o meno, è per dare l’idea). Per questo motivo, serve un metodo che permetta di conservare questo legame di causalità nonostante la partizione dell’input, ed è proprio qui che entrano in gioco OLA e OLS.

OverLap and Add (OLA)

E’ un algoritmo di convoluzione che implementa proprio il principio descritto sopra. Andiamo subito alla descrizione passo per passo con un esempio, perché ne renderà più intuitiva la comprensione.

Consideriamo la seguente situazione:

Filtro lungo \(M=4\) campioni;
Segnale uguale a \(x[n]=\{1,2,3,4,5,-1,-2,-3,-4,-5\}\);
Partizioni del segnale lunghe \(L=5\) campioni (in pratica processiamo 5 samples in input per volta).

Con questi dati immaginando di convolvere, una partizione per volta, il segnale per il filtro: otterremmo degli output di lunghezza \(L+M-1=8\) samples. Dobbiamo quindi impostare una lunghezza dei frames \(N>=L+M-1\): in questo caso scegliamo proprio \(N=8\).

Conoscendo ciò, procediamo con il primo passo, ovvero il padding (capiremo durante l’ultimo step l’utilità di questo passaggio):

Una volta che il filtro e il frame hanno la stessa lunghezza temporale \(N\), possiamo passare al dominio della frequenza eseguendo la FFT sui singoli frames (nota: nelle immagini, indico i risultati dei vari stadi con simboli e colori: per comprendere l’algoritmo non è necessario conoscere il valore dei samples, basta comprendere il flusso del processamento).

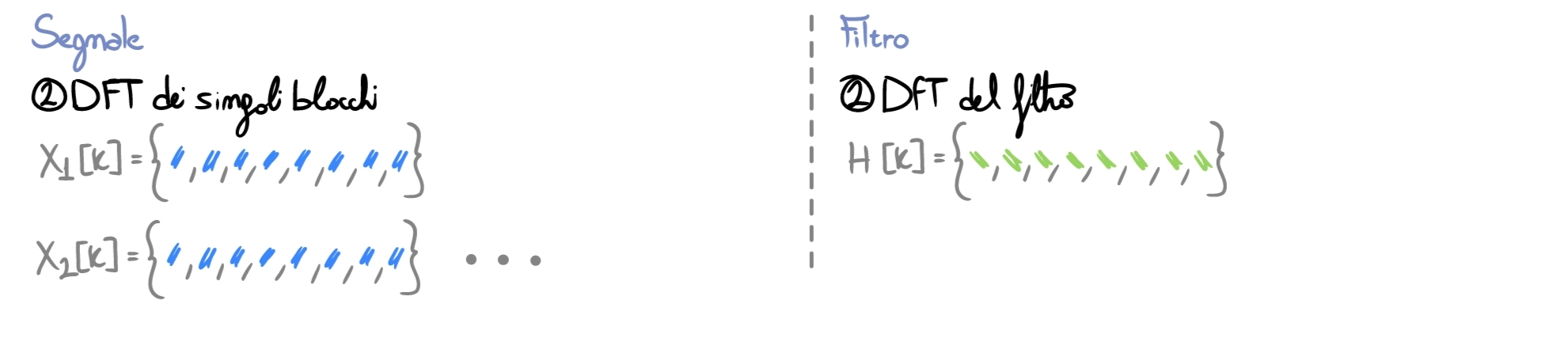
Adesso eseguiamo il filtering vero e proprio: convolvere nel tempo = moltiplicare sample per sample in frequenza. Una volta finito, torniamo al dominio del tempo tramite IDFT.

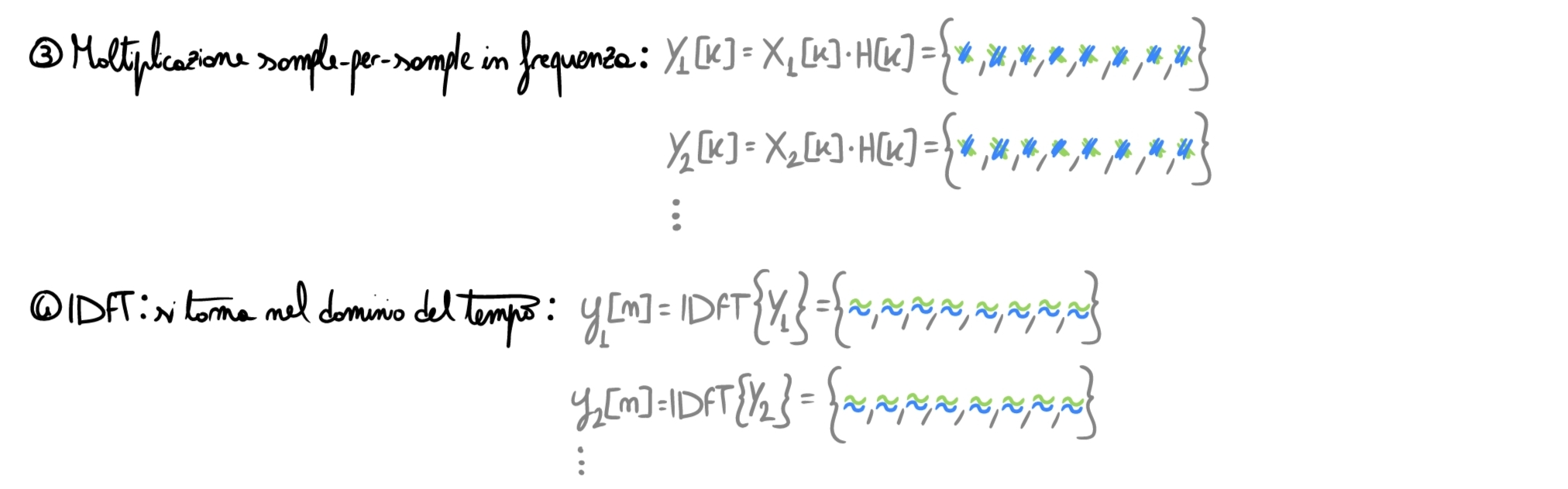
E’ giunto ora il momento cruciale: dobbiamo unire i frames tra loro e capire perché abbiamo paddato all’inizio.

Facciamo un confronto con una convoluzione “standard”: lunghezza segnale processato \(= 10\) samples, lunghezza filtro \(=4\) samples, per cui il segnale di output sarà lungo \(L=10+4-1=13\) samples.

Se mettessimo uno di seguito all’altro i frames \(y_i[n]\) calcolati, otterremmo un segnale lungo \(16\): qualcosa non va.

Il fatto è che il padding effettuato all’inizio è pensato per contenere l’effetto del wrap around: come visto nell’articolo sulla convoluzione, assumere che un segnale sia discreto in frequenza consiste nel considerarlo periodico nel dominio del tempo (il segnale/frame si ripete all’infinito). La convoluzione che si effettua tramite DFT è quindi circolare, e lo zero-padding serve proprio a contenere la coda della convoluzione che, altrimenti, andrebbe a corrompere i samples iniziali. L’informazione degli ultimi \(M-1\) samples del frame a \(t=n-1\) va pertanto sommata a quella dei primi \(M-1\) samples del frame successivo \(t=n\), in modo da ricostruire l’intero output di quella che sarebbe una convoluzione lineare. In pratica si sovrappongono i frames in questo modo:

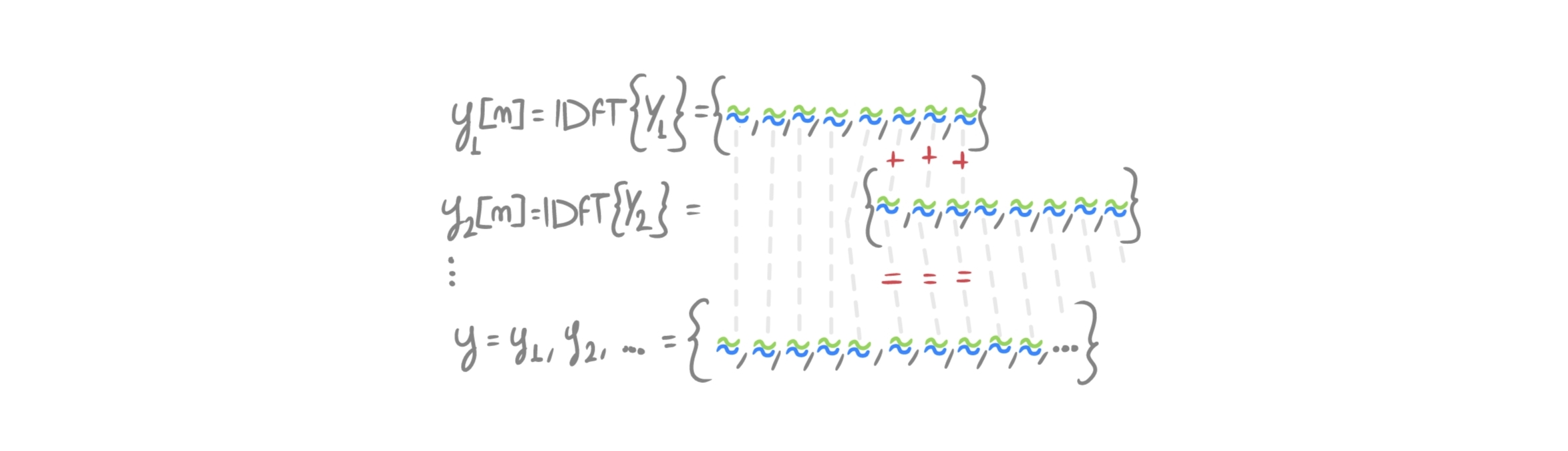
Non siamo convinti del risultato? Proviamo a fare un semplice esempio, a mano, nel dominio del tempo.

Considerando il segnale \(x[n]=\{1,2,3,2\}\) e il filtro \(h[n]=\{2,1,4,2\}\), iniziamo con le operazioni preliminari al calcolo:

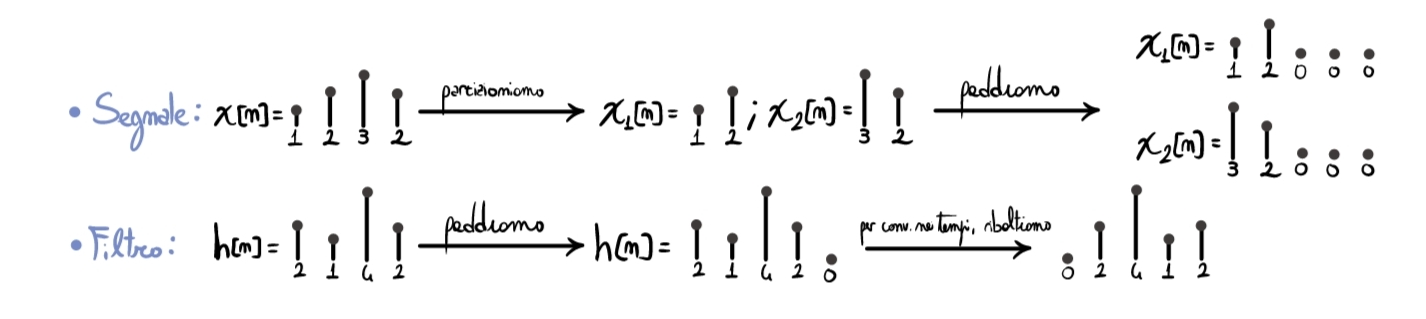
Adesso possiamo effettuare il resto dei calcoli:

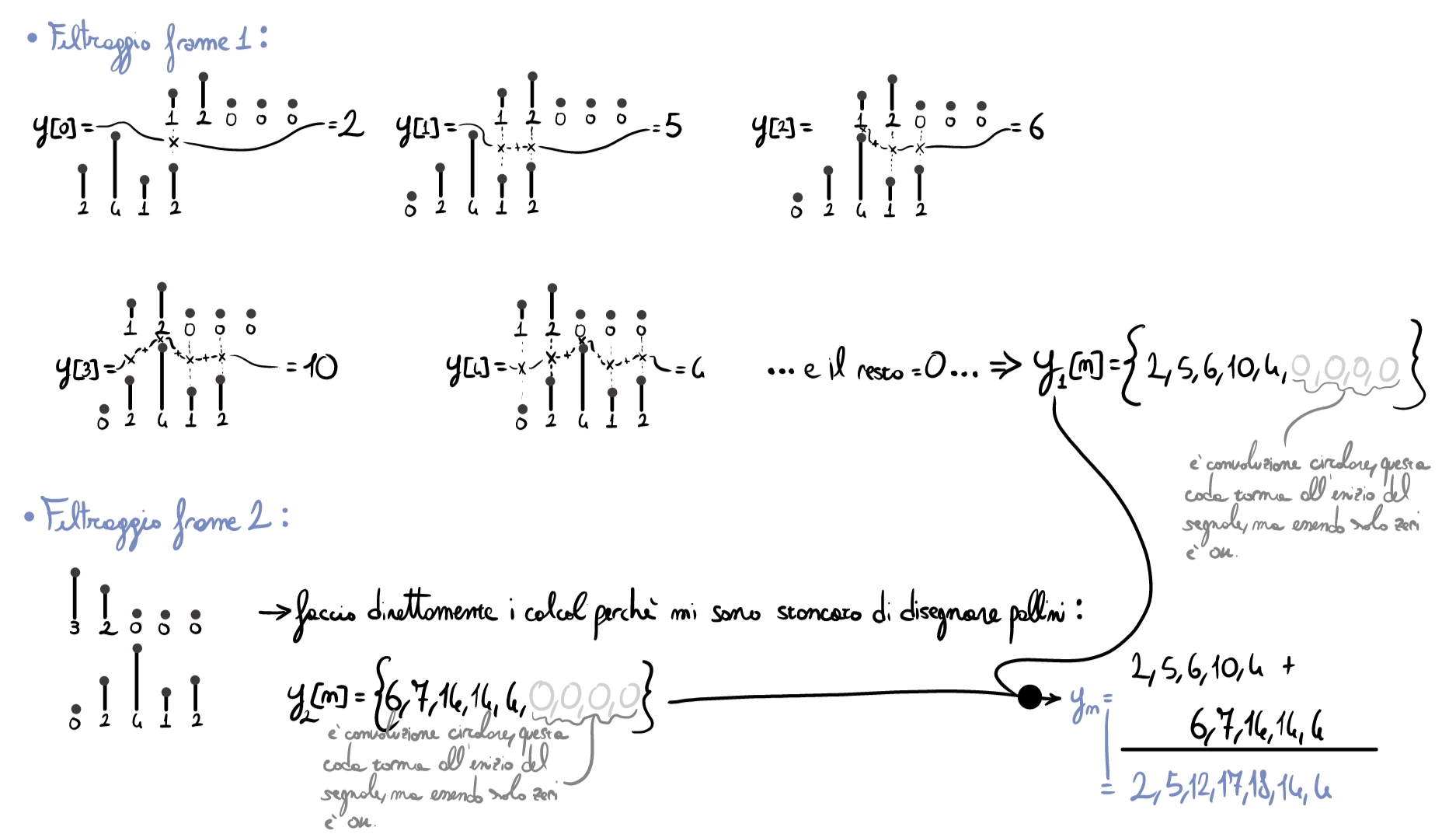
Eseguendo una semplice convoluzione lineare, otterremmo lo stesso risultato.

OverLap and Save (OLS)

E’ una tecnica molto simile alla precedente in cui però nel passaggio finale, invece che sovrapporre e sommare, si scarta una parte dei samples di output poiché corrotti dalla convoluzione circolare. Analizziamo anche in questo caso l’algoritmo passo per passo.

Consideriamo il medesimo esempio del precedente caso OLA:

Filtro lungo \(M=4\) campioni;
Segnale uguale a \(x[n]=\{1,2,3,4,5,-1,-2,-3,-4,-5\}\);
Partizioni del segnale lunghi \(L=5\) campioni.
Output conv. filtro \(*\) Partizione segnale pari a \(N>=L+M-1\) samples. Scegliamo anche in questo caso la lunghezza del frame pari a \(N=8\).

Il primo passo consiste in:

paddare il frame corrente del segnale con gli ultimi \(M-1\) samples del frame precedente;
effettuare lo zero-padding del filtro come già visto precedentemente.

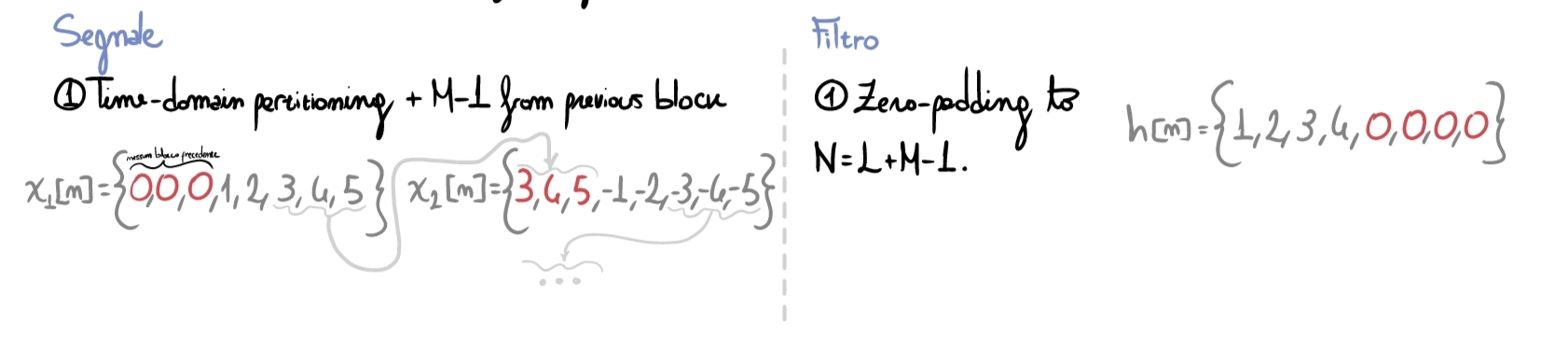
Passiamo poi al dominio delle frequenze, filtrando e tornando al dominio del tempo come già visto:

Ci troviamo quindi al passaggio cardine dell’algoritmo: dobbiamo capire come rimettere insieme i vari pezzi di output. Durante il primo step abbiamo “allungato” ogni frame incollando a sinistra gli \(M-1\) samples del frame precedente: questo ha permesso di

“Portarci dietro” l’informazione dei samples passati che ancora incide sui samples del blocco in input corrente;
Usare i primi \(M-1\) samples come “contenitori” per il fenomeno del wrap aound.

Per questo, ora dobbiamo semplicemente scartare quegli \(M-1\) samples iniziali corrotti dalla coda della convoluzione circolare e fondere di nuovo insieme i frames ottenuti:

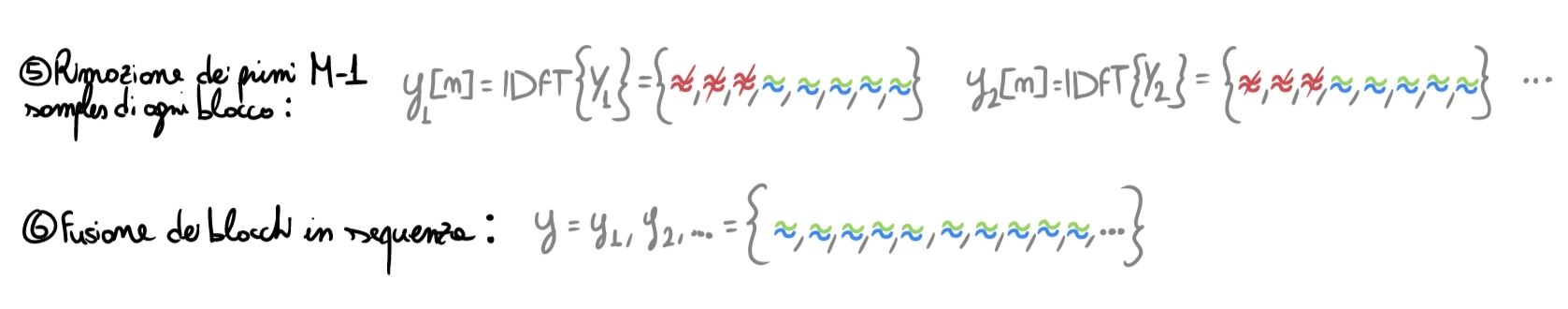
Per maggior chiarezza, ho provato a rappresentare graficamente il perché sia necessario aggiungere i samples passati all’inizio di ogni frame. I numeri (1,2,3) rappresentano l’ordine temporale in cui i vari eventi accadono durante la convoluzione.

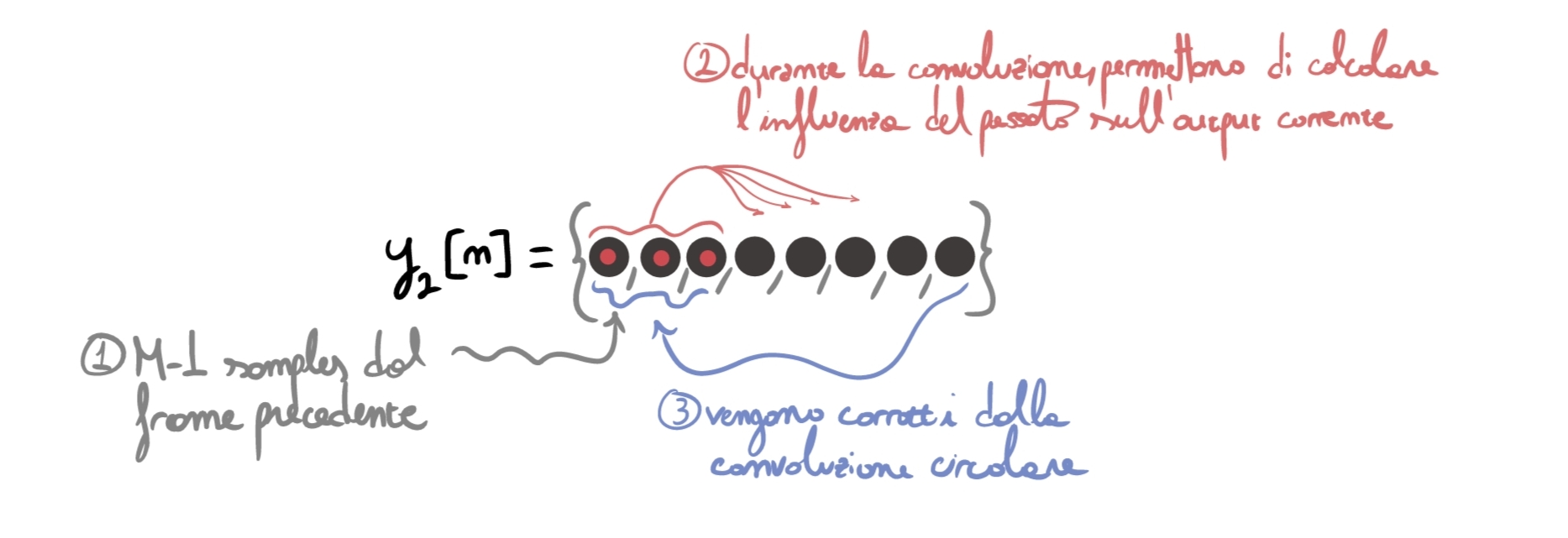
Partitioned Convolution

Negli algoritmi visti sopra, abbiamo utilizzato un filtro molto corto. Immaginiamo ora il caso in cui si voglia convolvere il segnale in ingresso con un Impulse Response molto lungo, oltre \(16.000\) samples. Partizionare il segnale audio non è abbastanza: per ogni frame ci toccherebbe paddare fino a \(N=L+M-1=\) più di \(16k\) samples, poi eseguire in RT la FFT di questo gigantesco frame, moltiplicare sample per sample e poi ritornare nei tempi. Un carico di lavoro enorme che genererebbe molta latenza.

Come risolviamo allora? Beh, partizioniamo anche il filtro ed effettuiamo il minor numero di operazioni possibili in real time.

1. Operazioni offline

Effettuiamo tutte le operazioni che non necessitano di essere svolte in Real Time, così da alleggerire il più possibile il carico sul sistema nel momento cruciale dell’esecuzione.

Prima di tutto prepariamo il filtro. Decidiamo la lunghezza \(P\) delle partizioni (sia di quelli del segnale che di quelli del filtro) e partizioniamo il filtro in \(K=L/P\) partizioni, dove \(L\) è la lunghezza del filtro intero. Paddiamo ogni partizione fino alla lunghezza dei bin della nostra FFT (maggiore della lunghezza dell’output della convoluzione, ovvero \(P_{signal}+P_{filter}-1=2P-1\)): ipotiziamo \(2P\).

Una volta ottenute le \(K\) partizioni, effettuiamo la FFT per ognuna di esse così da aver già questi risultati parziali pronti per il calcolo in RT.

Prepariamoci anche alcune strutture che ci serviranno in seguito:

un buffer lungo \(2P\) che costituirà il nostro frame, la cui prima metà di celle è inizializzata con degli zeri;
una coda chiamata FDL = Frequency Delay Line, che servirà a memorizzare i frames passati (in frequenza) per calcolarne l’impatto sull’output corrente (vedremo in seguito).

2. Operazioni in RT

Ok, siamo live. Il chitarrista accende il pedale ed inizia a suonare sulla sua Stratocaster. I samples iniziano a fluire dal cavo verso il nostro pedale, e iniziamo ad accumularli nel buffer:

Nota: i primi \(P\) samples sono:

\(0\) se stiamo processando il primo blocco audio (dato che non c’erano blocchi audio precedenti);
Gli ultimi \(P\) samples del frame precedente se stiamo procedando un qualsiasi frame che non sia il primo. E’ in pratica lo stesso passo che abbiamo visto nell’algoritmo OLS.

Una volta completata la ricezione del frame, si calcola la sua FFT \(X_i[k]=FFT\{frame_i\}\) e la si salva nella FDL:

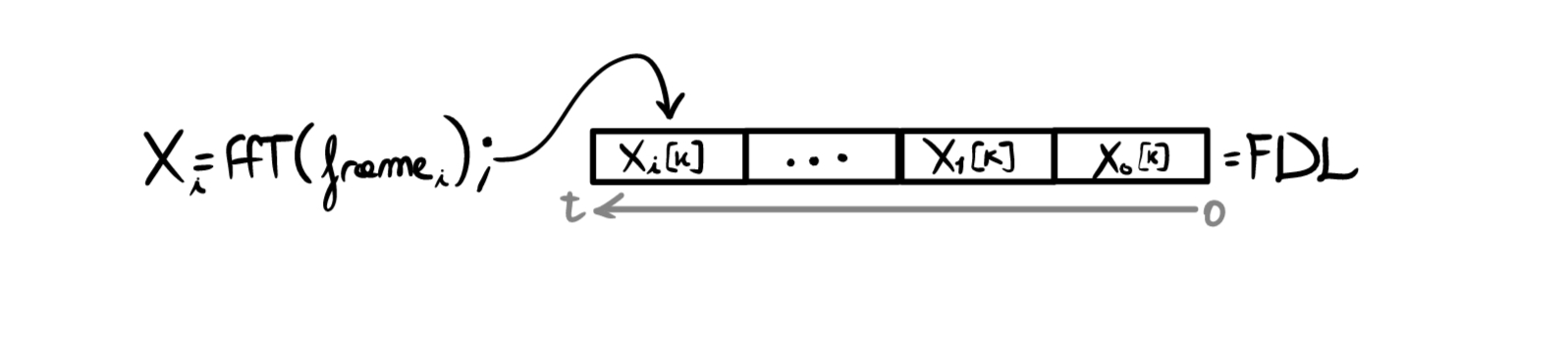
A questo punto ci ritroviamo con FDL \(= \{X_0[k], X_1[k], ... ,X_i[k]\}\) che rappresenta il nostro input, \(H=\{H_0[k], H_1[k],...H_K[k]\}\) che rappresenta il filtro e vogliamo ottenere il frame di output corrente \(Y_i[k]\).

Per rendere più facile la comprensione, consideriamo il caso specifico con \(K=4\), in cui ad un certo istante \(t\) abbiamo già emesso \(6\) frames di output e dobbiamo elaborare il settimo frame in input (con le fasi precedenti già completate).

Per applicare il filtro partizionato dobbiamo “ricomporre la convoluzione temporalmente”, e quindi “convolvere i frames di segnale più recenti con le parti iniziali dell’IR, mentre i frames precedenti del segnale con blocchi di IR successivi (se ci pensate, è proprio quello che accadrebbe se non partizionassimo la convoluzione):

La parte più complessa è passata; da qui in poi procediamo come un semplice OLS:

Eseguiamo la \(IFFT\) del frame, tornando al dominio del tempo;
Eliminiamo i primi \(P\) samples (similmente a quanto visto nell’algoritmo OLS);
Mandiamo in output il resto dei samples (ovvero ricostruiamo l’output mettendo i frames uno di seguito all’altro).

(Sarebbe stato possibile implementare lo stesso algoritmo usando OLA).

La domanda che potrebbe sorgere adesso è: ok, ma in cosa stiamo risparmiando? Stiamo comunque usando l’interezza del filtro, cosa sarebbe cambiato nell’effettuare la convoluzione con un semplice OLS o OLA?

La risposta sta nella percentuale di operazioni che possiamo precomputare offline e quelle che siamo forzati ad effettuare in real time:

nel caso di OLS/OLA possiamo precomputare il zero-padding e la FFT del filtro, ma dobbiamo per forza eseguire padding (fino a \(N=L*M-1\)) + FFT (di un frame lungo \(N\), che nel caso \(M\) sia molto oungo, diventa molto costoso), le moltiplicazioni samples per samples in frequenza e poi il ritorno nei tempi con la sovrapposizione o lo scarto dei “samples di transizione” tra i frames.
nel caso della partitioned convolution possiamo non soltanto pre-computare le partizioni del filtro come nel caso sopra, ma possiamo anche usare frames molto più corti dato che \(P\) non è vincolato inferiormente dalla lunghezza del filtro intero (es. se il filtro è lungo \(16k\) samples, con OLA dobbiamo usare frames di lunghezza \(16k + L_{\text{part. sign.}}-1\), mentre con la partitioned convolution non siamo vincolati dalla lunghezza \(16k\) del filtro perché possiamo partizionarlo in blocchi molto più piccoli). Questo vuol dire che le FFT che dobbiamo effettuare in real-time sono molto corte, perché il resto dei frames in frequenza li abbiamo salvati nella FDL e l’unica cosa che dobbiamo fare è moltiplicare sample per sample in frequenza e poi tornare nei tempi.

In pratica, si ha molto meno carico computazionale dal punto di vista di FFT e IFFT per singolo blocco, così da abbasssare drasticamente la latenza dell’output se il filtro è molto lungo.

Angelo Antona, 15 DICEMBRE 2025