Toolbox per studiare DSP

Possiamo vedere un segnale come un oggetto (funzione) che trasporta informazione. Il tizio polacco di Starbucks che in questo preciso momento sta ulrando parole da me incomprensibili, cercando di comunicarmi che il caffè è pronto, sta tentando di trasmettere un’informazione (il caffè è pronto) attraverso un segnale (urla).

Immaginando che il tizio di Starbucks sia un usignolo e stia cantandomi una singola nota, potremmo rappresentare le sue urla come una sinusoide a frequenza fissa \(x(t)=A*cos(2*\pi*t+\phi)\), dove \(A\) è l’ampiezza (intensità delle urla), \(t\) è il tempo e \(\phi\) è la fase (ne parleremo a breve).

La funzione altro non è che una mappa tra i livelli di ampiezza assunti da segnale ed il tempo \(t\). Se tale mappatura è continua nel tempo, e quindi vi sono campioni per ogni infinitesimo istante di tempo, allora il segnale è continuo (qualsiasi suono che possiamo percepire), altrimenti è discreto.

La fase è un concetto leggermente più complesso da comprendere: se consideriamo un segnale \(x(t)=cos(2*\pi*t)\), esso ha fase \(\phi=0\) e, dato che \(cos(0)=1\), esso varrà \(1\) per \(t=0\). Se però aggiungiamo una fase, per esempio \(\phi=-\frac{\pi}{2}\), ecco che otteniamo il segnale \(x'(t)=cos(2*\pi*t-\frac{\pi}{2})\), che è uguale a dire \(x'(t)=cos(2*\pi*(t-\frac{1}{4})\). E’ facile notare come il \(t-\frac{1}{4}\) indichi un ritardo applicato al segnale. Ecco, la fase rappresenta un anticipo/ritardo applicato al segnale, una traslazione sull’asse del tempo.

Crearsi l’immagine mentale della fase di una singola sinusoide è abbastanza semplice, ma la situazione diventa problematica quando dobbiamo analizzare segnali più complessi. In tal caso, come vedremo in seguito, ci verrà in aiuto il caro Fourier, grazie al quale possiamo supporre di scomporre qualsiasi segnale nella somma di (un numero infinito di) semplici sinusoidi, ognuna con la propria ampiezza e la propria fase. E’ possibile in tal caso ottenere un’immagine comprensibile delle caratteristiche del segnale trasformandolo in frequenza e disegnando i diagrammi di modulo e fase. Non c’hai capito niente? Fa niente, lo spiegheremo nel dettaglio in seguito.

Partiamo dalle basi basi basi

Prima di cominciare con la trattazione vera e propria, ripassiamo un po’ di concetti che sicuramente conosciamo già ma che il tempo potrebbe aver reso sfocati nella nostra mente.

I numeri

I numeri sono compagni fidati di noi scimmie glabre da molto, molto tempo. Ci sono venuti in soccorso man mano che la nostra società si evolveva e le cose di cui (letteralmente) tener conto aumentavano. Proviamo a stilare una breve timeline.

Numeri naturali: sono semplicemente i numeri interi positivi (1, 2, 3, 4, …) e li usiamo sin dall’inizio della civiltà. Esistono per esempio tavolette di magazzini babilonesi ed egizi in cui si teneva il conto dell’inventario.
Numeri interi: in pratica è l’insieme dei naturali con l’aggiunta dei negativi (ovvero \(..., -3, -2, -1, 0, 1, 2, 3, ...\)). Nonostante possano sembrare intuitivi a noi uomini del 21esimo secolo, il concetto di numero negativo è stato per lungo tempo di difficile comprensione (una quantità più piccola del niente): se, come detto, i naturali sono stati utilizzati sin dalle più antiche civiltà (quindi più di 5000 anni fa), i numeri negativi compaiono in testi matematici solo molti secoli dopo, formalizzati in India intorno al VII secolo d.C. e accettati in Europa ancora più tardi.
Numeri razionali: anche questi, adoperati sin dalle prime civiltà, sono nati per gestire la suddivisione di proprietà e terreni. Per intenderci, sono i numeri frazionari del tipo \(\frac{5}{4}\), \(\frac{1}{2}\) e qualsiasi altra frazione con numeratore e denominatore interi (e \(\text{den}\neq 0\)).
Numeri irrazionali: sei un matematico greco che vive in Calabria, a Crotone, nel V secolo a.C.. Non c’è ancora la ‘Ndrangheta, per cui decidi di unirti ai Pitagorici. Vivi beato nel tuo mondo di numeri razionali (chiamati così appunto per questo) e tutto è perfetto, legato da semplici relazioni tra grandezze (frazioni con numeratore e denominatore interi e \(\text{den}\neq 0\)). Un bel giorno, il tuo amico Ippaso da Metaponto ti chiede di calcolare quanto è lunga la diagonale di un quadrato di lato 1. Hai sempre saputo che era un tipo strano, ma decidi comunque di assecondare la sua richiesta. Se consideriamo la metà di quadrato delimitata dalla diagonale e due lati, quello che otteniamo è un triangolo rettangolo. La soluzione è quindi facilissima (ed autoreferenziale, per un pitagorico): il teorema di Pitagora! Ok, quindi \(\text{diag}^2=\text{lato}^2+\text{lato}^2\), e quindi \(1^2+1^2=2\): la soluzione è \(\text{diag}=\sqrt{2}\). Aspetta, ma che numero è \(\sqrt{2}\)? Posso esprimerlo sotto forma di frazione? Deve essere così, dato che la realtà è fatta solo di relazioni tra grandezze, no? Come scopriranno, purtroppo no. Ed ecco comparire una nuova specie di numeri: gli irrazionali. Per secoli, i matematici hanno “procrastinato” nel dare una definizione rigorosa di tale classe, usando piuttosto arzigogolamenti geometrici per arrivare agli stessi risultati.
Numeri reali: mettendo insieme numeri razionali e irrazionali otteniamo i numeri reali, che possiamo immaginare come tutti i punti di una retta continua. Di fatto li si usa, in forma implicita, da millenni, ma una definizione rigorosa di questo insieme arriva solo nel XIX secolo, con il lavoro di matematici come Dedekind e Cantor.
Numeri complessi: la matematica è andata avanti e spesso, tra i calcoli, ci si ritrovava ad aver a che fare con radici di numeri negativi (es. la soluzione di \(x^2+1=0\)). Per secoli, gli scienziati hanno trattato questi valori come numeri “immaginari” (nomenclatura poi rimasta), cioè utili per i calcoli ma “non esistenti per davvero”. Tra XVI e XVII secolo, nel tentativo di risolvere equazioni di grado superiore al secondo, matematici come Cardano e Bombelli iniziano a usarli in modo sistematico; nel XVIII secolo Euler li maneggia con grande naturalezza, e tra fine XVIII e inizio XIX secolo, con Argand e Gauss, si smette di pensare a tali numeri come un “trucco” e li si tratta come un vero oggetto matematico e geometrico.

Per avere un’idea più chiara delle relazioni tra gli insiemi sopracitati, ecco qui un diagramma preso da Wikipedia:

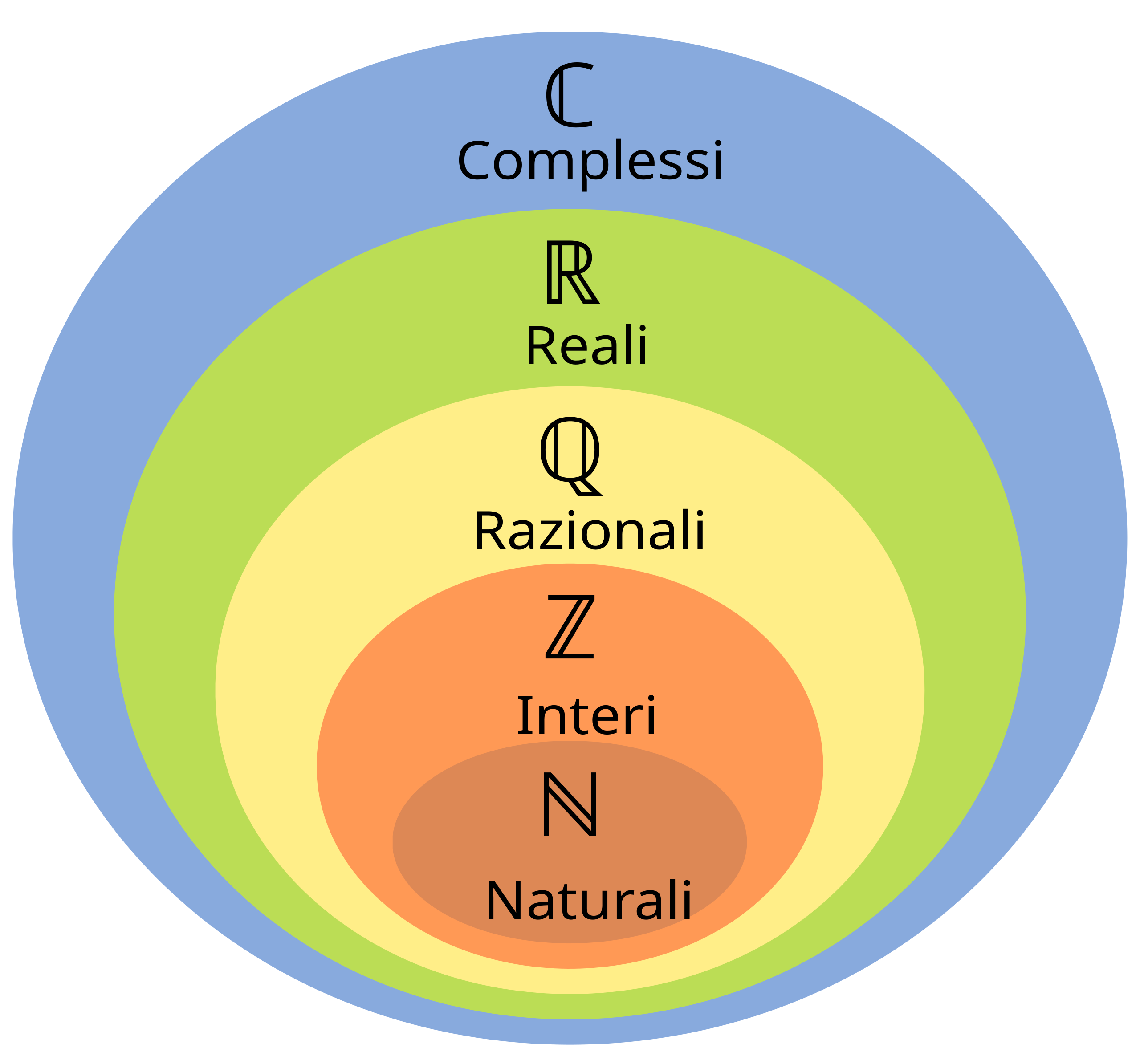
Numeri

Dando per scontato che il lettore abbia familiarità coi numeri naturali, reali, razionali e irrazionali , scriverò solo un breve ripasso degli immaginari.

Numeri immaginari e complessi

I numeri reali rappresentati nel diagramma in alto hanno un grande limite strutturale: non permettono di calcolare radici di numeri negativi, come per esempio \(\sqrt{-1}\). Per ovviare a ciò, definiamo un’unità immaginaria \(i=\sqrt{-1}\). Questo è il mattone fondamentale dei numeri immaginari: qualsiasi numero \(b*i\) con \(b\in\mathbb{R}\), è un numero (puramente) immaginario.

Definiamo quindi l’insieme dei numeri complessi come quello che contiene i numeri che hanno forma \(a + b * i\), con \(a\in\mathbb{R}\) e \(b*i\in \mathbb{I}\).

La rappresentazione di tali numeri avviene su un grafico cartesiano chiamato “diagramma di Argand-Gauss”, in cui semplicemente si rappresenta sull’asse \(x\) la parte reale e sull’asse \(y\) quella immaginaria, ricavando da tali coordinate un punto sul piano.

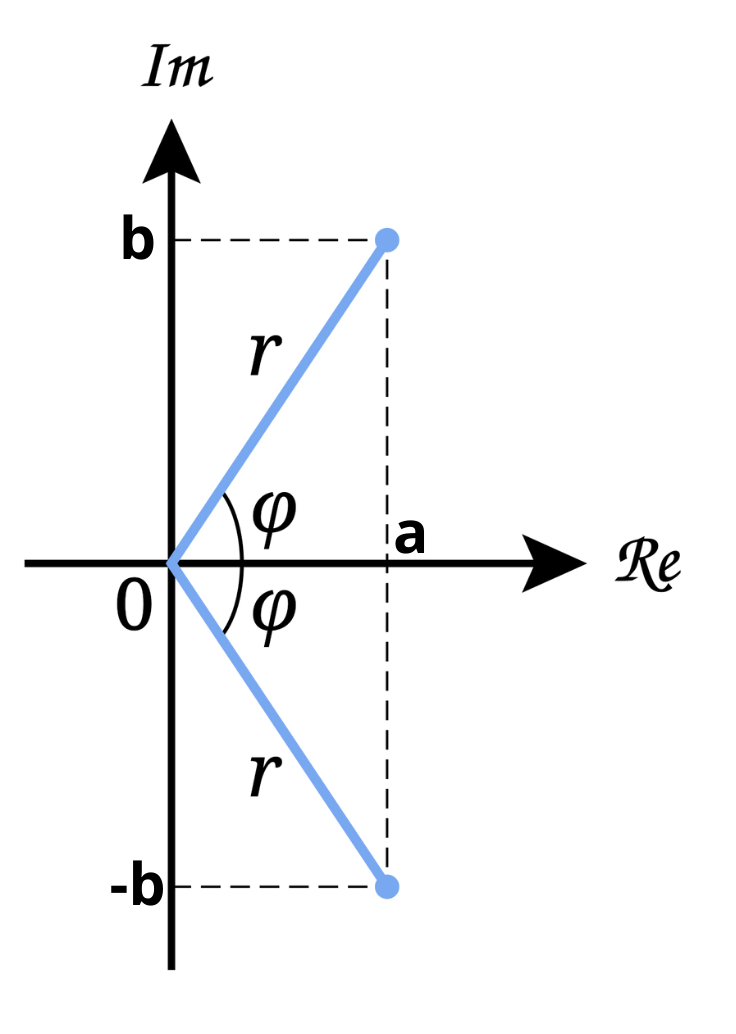
Piano Gauss

Il segmento che unisce l’origine degli assi al punto ricavato è detto norma e si calcola come \(r=\sqrt{a^2+b^2}\). L’angolo \(\theta\) nell’immagine è la fase, e la si può ricavare dalla relazione \(b/a=\tan{\theta}\)

E’ possibile rappresentare uno stesso numero complesso attraverso diverse forme di scrittura:

Forma algebrica: è quella vista sopra, dove si rappresenta il numero come somma tra la sua parte reale e quella complessa (\(c=a+b*i\) dove \(a,b\in\mathbb{R}\) e \(i=\) immaginario puro).
Forma trigonometrica: calcolando il modulo e la fase de numero complesso \(c\) del punto precedente attraverso le già viste formule \(r=\sqrt{a^2+b^2}\) e \(\theta=tan(b/a)\), possiamo rappresentare la stessa quantità attraverso la forma \(c=r*[cos(\theta)+i*sin(\theta)]\). Ovviamente, è sempre possibile tornare alla forma algebrica considerando \(a=r*cos(\theta)\) e \(b=i*sin(\theta)\).
Forma esponenziale: usando \(\theta, r\) calcolati nel punto precedente, è possibile esprimere \(c\) attraverso la cosidetta forma “esponenziale”: \(c=r*e^{\theta*i}\).

Ognuna delle forme viste ha dei casi d’uso specifici, nei quali essa risulta più comoda delle altre.

Alcune definizioni importanti che reincontreremo in seguito sono:

Complesso coniugato: dato un numero \(c=a+b*i\), si dice che il numero \(c^*=a-b*i\) è il suo complesso coniugato (parte immaginaria di segno opposto).
Radici \(n\)-esime: nel campo dei complessi, una radice \(n-\)esima ha precisamente \(n\) soluzioni. Per capire il concetto, facciamo un esempio. Consideriamo il numero \(c=-2+2i\) e scriviamolo in forma esponenziale (\(\theta=tan(b/a)\) e \(r=\sqrt{a^2+b^2}\)). Poniamoci l’obiettivo di calcolare la radice \(\sqrt{c}^3=c^{1/3}\). L’equazione diventa \(c^{1/3}=r^{1/3}*e^{\frac{\theta}{3}*i}\) e, sostituendo i valori numerici, \(c^{1/3}=8^{1/6}*e^{\frac{135^\circ}{3}*i}\), e quindi \(\sqrt{c}^3=\sqrt{2}*e^{45^\circ*i}\). Questa appena trovata è solo una delle \(n=3\) soluzioni. Considerando il cerchio sul piano di Gauss, le altre due si troveranno a periodicità \(P=\frac{2\pi}{n}\) che in questo caso è \(P=\frac{2\pi}{3}=120^\circ\). Possiamo visualizzare ciò che abbiamo detto nell’immagine qui sotto:

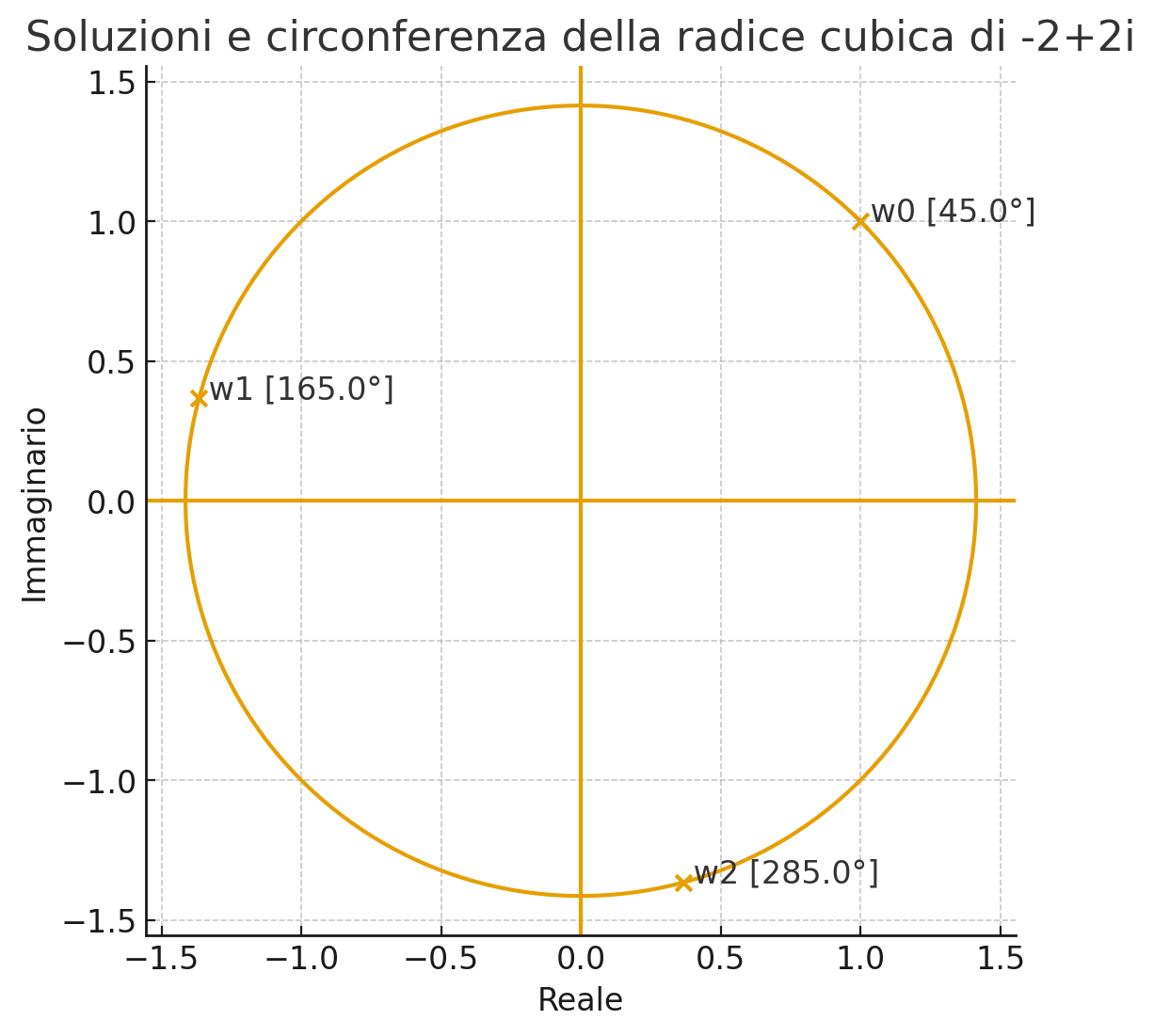
Radici n-esime

Trigonometria

Sarà utile ricordare alcune delle vecchie e noiose formule di trigonometria:

\(sin(a ± b) = sin(a)* cos(b) ± cos(a)* sin(b)\);
\(cos(a ± b) = cos(a) *cos(b) ∓ sin (a)*sin(b)\);
\(sin(2t) = 2 sin(t) *cos(t)\);
\(cos(2t) = cos^2(t) − sin^2(t)\);
\(sin^2(t) = \frac{1 − cos(2t)}{2}\);
\(cos²t = \frac{1 + cos(2t)}{2}\).

Successioni

Una successione è una funzione discreta che associa ad ogni indice \(n\) un numero. Per esempio, la successione \(a_n=\frac{1}{n}\) con \(n=1,2,3,...\) consiste nella sequenza dei valori \(1,\frac{1}{2},\frac{1}{3},...\).

Un concetto molto importante è quello di limite di una successione: dire che \(\lim_{n\to\infty} a_n = L\) vuol dire che, man mano che aumentiamo l’indice n, il valore della successione assomiglia sempre di più ad \(L\).

Dal concetto di limite deriva quello di convergenza della successione: se una successione tende ad un valore finito ben specifico, allora si dice che converge a quel valore. Ci sono alcuni casi notevoli da ricordare:

Successione geometrica: è del tipo \(a_n=r^n\). Una successione del genere:
- converge a \(0\) se \(\|r\|<1\);
- converge a \(1\) se \(r=1\);
- è indeterminata se se \(r<-1\);
- diverge in modulo se \(r \le -1\).
Successione polinomiale: è del tipo \(a_n=n^p\). In tal caso, la successione diverge se \(p>0\).

Vi sono poi dei “rapporti di forza” tra queste successione: se moltiplichiamo una geometrica con una esponenziale, la successione risultante seguirà l’andamento dell’esponenziale, poiché quest’ultima cresce/decresce più rapidamente della geometrica.

Serie

A partire dalle successioni possiamo definire le serie come somma infinita di tutti i termini di una successione: \(S_N=\sum_{n=n_0}^{N} a_n\). Si dice che la serie converge se \(\lim_{N\to\infty} S_N = S\), con \(S\) finito. Se tale limite non esiste o è infinito, allora la serie diverge.

Data una serie \(\sum a_n\), si distinguono poi due tipi di convergenza:

Convergenza assoluta se converge la serie \(\sum_{n=n_0}^{\infty} \|a_n\| < \infty\) (in pratica converge la serie del velore assoluto della successione \(a_n\));
Convergenza condizionata: se la serie \(\sum_{n=n_0}^{\infty} a_n < \infty\) converge, ma la serie \(\sum_{n=n_0}^{\infty} \|a_n\| < \infty\) diverge. In tal caso la convergenza è più debole (es. la serie con argomento \(a_n=\frac{-1^n}{n}\) converge, ma quella con argomento \(\|a_n\|=\frac{1^n}{n}\) diverge).

Ok, ma come facciamo praticamente a capire se una serie converge o meno? Non è sempre facile, ma possiamo affidarci ad alcuni trucchetti:

Condizione necessaria (ma non sufficiente) affinché una serie converga è che la successione che essa contiene converga a 0. Se quindi incontriamo una serie la cui successione non va a 0, non dobbiamo neanche perderci tempo: diverge.
Confronto con serie nota: immaginiamo di avere due serie \(\sum{a_n}\) e \(\sum{b_n}\). Conosciamo già \(\sum{a_n}\) e sappiamo che converge. Vogliamo capire se anche \(\sum{b_n}\) ha tale comportamento, ma non sappiamo come fare. Beh, se siamo così fortunati da avere che \(\sum{b_n}<\sum{a_n}\), allora possiamo subito concludere che anche \(\sum{b_n}\) converge.
Confronto asintotico: date due serie \(\sum{a_n}\) e \(\sum{b_n}\), entrambe \(>0\), se \(\lim_{n\to\infty}\frac{a_n}{b_n}=c\), con \(0<c<\infty\), allora o convergono entrambe o divergono entrambe. Ovviamente, lo scopo è quello di usare una serie nota che, messa in rapporto con l’altra in tale contesto, dia un limite finito: in tal modo potremo concludere che l’altra serie ha lo stesso comportamento della serie nota.
Test del rapporto: data una serie \(\sum{a_n}\), calcolando il rapporto \(L=\lim_{n\to\infty}\left\|\frac{a_{n+1}}{a_n}\right\|\) abbiamo che:
- se \(L<1\) essa converge assolutamente;
- se \(L=1\) non possiamo trarre alcuna conclusione da questo test;
- se \(L>1\) la serie diverge.
Test della radice: simile al precedente, questo test ci dice che data una serie \(\sum{a_n}\), calcolando \(L=\limsup_{n\to\infty}\sqrt[n]{\|a_n\|}\) è possibile dedurre che
- se \(L<1\) la serie converge assolutamente;
- se \(L=1\) non possiamo trarre conclusioni;
- se \(L>1\) la serie diverge.
Test alternato: data una serie a segno alterno, scrivibile nella forma \(\sum{(-1)^n*a_n}\), possiamo usare questo criterio di convergenza. Il test afferma che, se \(a_n\) è \(>=0\), monotona decrescente e tendente a \(0\), allora la serie complessiva converge.

Tutto molto bello. Ma come facciamo ad usare questi “criteri di comparazione” se non conosciamo alcuna serie nota? Il dubbio è lecito, ed infatti esistono molte serie “note” di cui si conosce l’andamento. Non scriverò una spiegazione dettagliata perché non è questo l’argomento principe del testo, ma è importante per i nostri scopi conoscere la serie geometrica, che ci tornerà molto utile in seguito.

In pratica, la serie geometrica è \(\sum_{n=0}^{\infty} r^n\) e converge se e solo se sono contemporaneamente verificate le seguenti condizioni:

\(\|r\|<1\);
\(\sum_{n=0}^{\infty} r^n = \frac{1}{1-r}\).

Esempio su serie e successioni

Consideriamo la serie \(\sum_{n=0}^{\infty} (-1)^n r^n\). Per quali \(r\) converge? Analizziamo prima di tutto il caso di \(r>0\).

Notando che \(r^n\) è una successione geometrica, possiamo dedurre che essa tende a \(0\) solo per \(\|r< 1\|\), mentre per valori \(=1\) essa converge a 1. Deduciamo quindi che il “vincolo destro” dell’insieme di convergenza è \(r< 1\). Vediamo che succede a sinistra:

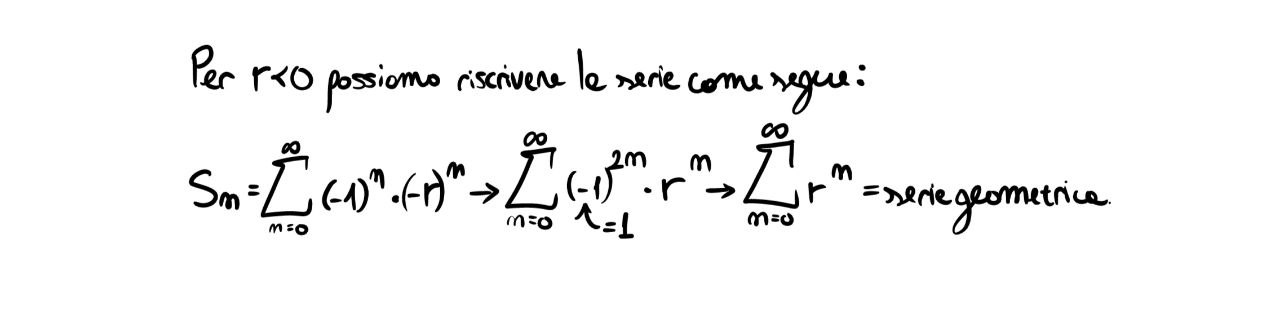
Come già visto, la serie sopra converge per \(\|r\|< 1\).

Si deduce in sintesi che la serie converge per valori di \(r \in (-1,1)\), estremi esclusi.

To be continued …

Non approfondirò ulteriormente gli argomenti visti sopra, nonostante siano stati trattati molto superficialmente ed in maniera incompleta, perché questo è stato solo un breve ripasso propedeutico alla comprensione dell’articolo sulla convoluzione.

Angelo Antona, 3 DICEMBRE 2025